Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example 1:
Input: "babad" Output: "bab" Note: "aba" is also a valid answer.
Example 2:
Input: "cbbd" Output: "bb"
class Solution {
public String longestPalindrome(String s) {
}
}
Problem Clarification
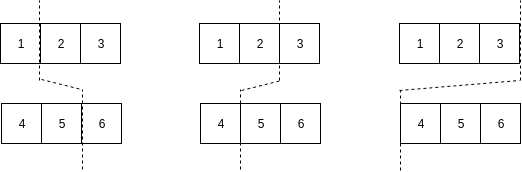
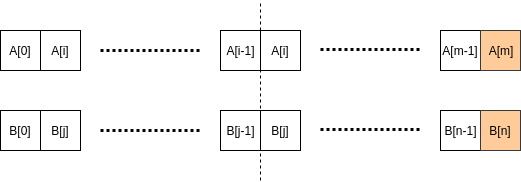
The longest palindromic substring must have characters that are adjacent in the original string.Idea - 1
We can check each of the
substrings and see if it is palindromic in 
time and keep track of the longest among them.
Total time is 
and space is 
.
class Solution {
public String longestPalindrome(String s) {
int n = s.length();
if(n == 0)
{
return "";
}
int maxLength = 1;
int longestStart = 0, longestEnd = 0;
for(int i = 0; i < n-1; ++i)
{
for(int j = i+1; j < n; ++j)
{
if(palindromic(s, i, j) && j-i+1 > maxLength)
{
maxLength = j-i+1;
longestStart = i;
longestEnd = j;
}
}
}
return s.substring(longestStart, longestEnd+1);
}
private boolean palindromic(String s, int begin, int end)
{
while(begin < end)
{
if(s.charAt(begin) != s.charAt(end))
{
return false;
}
++begin;
--end;
}
return true;
}
}
Runtime: 1541 ms, faster than 5.00% of Java online submissions for Longest Palindromic Substring.
Memory Usage: 37.3 MB, less than 94.27% of Java online submissions for Longest Palindromic Substring.Idea - 2
If
is a palindrome, then it follows that 
and 
is a palindrome. So, if we find out which 2-length substrings are palindrome then finding if a 4-length substring is a palindrome take time. So, overall we need to find which of the substrings are palindrome and each can be checked in time making overall time complexity and space complexity as well.
class Solution {
public String longestPalindrome(String s) {
int n = s.length();
if(n == 0)
{
return "";
}
boolean[][] dp = new boolean[n][n];
// all 1-length substrings are palindromes
for(int i = 0; i < n; ++i)
{
dp[i][i] = true;
}
int maxLength = 1;
int longestBegin = 0, longestEnd = 0;
for(int length = 2; length <= n; ++length)
{
int i = 0;
while(i+length <= n)
{
int j = i+length-1;
// i-th and j-th char match and these are the only chars or
// the in between chars form palindrome
if(s.charAt(i)==s.charAt(j) && ( i+1 > j-1 || dp[i+1][j-1] ))
{
dp[i][j] = true;
if(length > maxLength)
{
maxLength = length;
longestBegin = i;
longestEnd = j;
}
}
++i;
}
}
return s.substring(longestBegin, longestEnd+1);
}
}
Runtime: 46 ms, faster than 40.03% of Java online submissions for Longest Palindromic Substring.
Memory Usage: 39.4 MB, less than 19.86% of Java online submissions for Longest Palindromic Substring.Idea - 3
A palindrome can be checked starting at two ends and going inwards or starting at a center going outwards. The latter approach has the benefit that there are only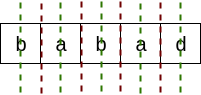 centers, so we end up with an algorithm with time and space .
Centers are of two types: falls on a character, falls between two characters.
class Solution {
class IndexPair
{
int i, j;
public IndexPair(int i, int j)
{
this.i = i;
this.j = j;
}
public int length()
{
return j-i+1;
}
}
public String longestPalindrome(String s) {
int n = s.length();
if(n == 0)
{
return "";
}
int maxLength = 1;
IndexPair sol = new IndexPair(0, 0);
for(int center = 0; center < n; ++center)
{
IndexPair candidate = longestFromCenter(s, center);
if(candidate.length() > sol.length())
{
sol = candidate;
}
}
return s.substring(sol.i, sol.j+1);
}
private IndexPair longestFromCenter(String s, int center)
{
int n = s.length();
// falls on a character
int left1 = center-1;
int right1 = center+1;
while(left1 >= 0 && right1 < n && s.charAt(left1)==s.charAt(right1))
{
--left1;
++right1;
}
int length1 = right1-left1-1;
// falls between two characters
int left2 = center-1;
int right2 = center;
while(left2 >= 0 && right2 < n && s.charAt(left2)==s.charAt(right2))
{
--left2;
++right2;
}
int length2 = right2-left2-1;
if(length1 > length2)
{
return new IndexPair(left1+1, right1-1);
}
else
{
return new IndexPair(left2+1, right2-1);
}
}
}
Runtime: 14 ms, faster than 64.48% of Java online submissions for Longest Palindromic Substring.
Memory Usage: 37.1 MB, less than 95.43% of Java online submissions for Longest Palindromic Substring.
time using the merge routine of mergesort. Suppose we have num1 = 
and num2 = 
. If we sorted the two arrays into one, we would have 
. Here, total number of elements is 5 and the middle element aka 
or the 3rd element (5) in the sorted order is the median. On the other hand, if we had num1 = 
and num2 = 
and the median would be the average of the middle element or 
rd element and the previous element. So, the median is 
. Clearly, if we take 
steps in the merge process and keep track of the currently selected element and the previous as well, we would have all information to compute median.
then we at least have the correct divide in terms of number of elements because i is the number of elements left of i-th index of the first array and j is the number of elements left of j-th index of second array, thus the left half of the divide has ![\max(\textrm{num1}[i-1],\ \textrm{nums2}[j-1])\ \le \min(\textrm{nums1}[i],\ \textrm{nums2}[j])](https://s0.wp.com/latex.php?latex=%5Cmax%28%5Ctextrm%7Bnum1%7D%5Bi-1%5D%2C%5C+%5Ctextrm%7Bnums2%7D%5Bj-1%5D%29%5C+%5Cle+%5Cmin%28%5Ctextrm%7Bnums1%7D%5Bi%5D%2C%5C+%5Ctextrm%7Bnums2%7D%5Bj%5D%29&bg=eae9e6&fg=363431&s=0&c=20201002)
, therefore the left half contains smaller elements and the right half contains bigger elements. For example, below all three division are valid in terms of size of the two halves, but only 3rd is the median divide.
.
We can actually iterate on [imin, imax] (intially imin=0 and imax=m) in binary search fashion and check if the divide is the median divide. Choosing nums1 as the shorter array gives us the desired time complexity of 
.
edges, so time complexity is 
. We use recursion, so worst case stack space is 
programmingpuzzles 