In a row of trees, the i-th tree produces fruit with type tree[i].

You start at any tree of your choice, then repeatedly perform the following steps:

1. Add one piece of fruit from this tree to your baskets.  If you cannot, stop.
2. Move to the next tree to the right of the current tree.  If there is no tree to the right, stop.

Note that you do not have any choice after the initial choice of starting tree: you must perform step 1, then step 2, then back to step 1, then step 2, and so on until you stop.

You have two baskets, and each basket can carry any quantity of fruit, but you want each basket to only carry one type of fruit each.

What is the total amount of fruit you can collect with this procedure?

Example 1:

Input: [1,2,1] 
Output: 3 
Explanation: We can collect [1,2,1]. 

Example 2:

Input: [0,1,2,2] 
Output: 3 
Explanation: We can collect [1,2,2]. If we started at the first tree, we would only collect [0, 1]. 

Example 3:

Input: [1,2,3,2,2] 
Output: 4 
Explanation: We can collect [2,3,2,2]. If we started at the first tree, we would only collect [1, 2]. 

Example 4:

Input: [3,3,3,1,2,1,1,2,3,3,4] 
Output: 5 
Explanation: We can collect [1,2,1,1,2]. If we started at the first tree or the eighth tree, we would only collect 4 fruits. 

Note:

1. 1 <= tree.length <= 40000
2. 0 <= tree[i] < tree.length

class Solution {
    public int totalFruit(int[] tree) {
        
    }
}

Problem Clarification

We need to find length of the longest subarray that contains at most 2 distinct numbers.

Idea - 1

We try each of the subarrays and check if the subarray contains only 2 distinct numbers. Time and space .

class Solution {
    public int totalFruit(int[] tree) {
        int n = tree.length;
        int max = 1;
        for(int len = n; len > 1; --len)
        {
            int i = 0;
            while(i+len <= n)
            {
                int j = i+len-1;
                if( containsAtMostTwo(tree, i, j) )
                {
                    return len;
                }
                
                ++i;
            }
        }
        
        return max;
    }
    
    private boolean containsAtMostTwo(int[] tree, int begin, int end)
    {
        HashSet<Integer> set = new HashSet<>();
        for(int i = begin; i <= end; ++i)
        {
            set.add(tree[i]);
            
            if(set.size() > 2)
            {
                return false;
            }
        }
        
        return true;
    }
}


Time limit exceeded on an input of size 3000.

Idea - 2

Starting with a window of 1-length window containing begin and end index [0, 0], we can try to grow it rightwards as long as adding the new element would not cause the window to have more than 2 distinct elements. When we see an element that we cannot add to the window, we can no longer grow the current window. Now we shrink as little as possible so that the window has copies of just one element so that we can add the new element. Thus the states we need to keep track of are: which two integers are in the current window, the last indices of the two integers in the current window and the beginning of the window.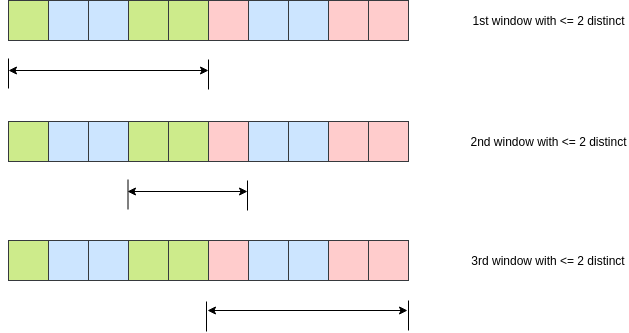

We have a time and space algorithm.

class Solution {
    public int totalFruit(int[] tree) {
        int n = tree.length;
        int startOfWindow = 0;
        int typeA = 0, typeB = 0;
        int maxLength = 0;
        int lastIndexOfTypeA = -1, lastIndexOfTypeB = -1;
        int i = 0;
        while(i < n)
        {
            if(lastIndexOfTypeA < 0)
            {
                lastIndexOfTypeA = i;
                typeA = tree[i];
            }
            else if(tree[i]==typeA)
            {
                lastIndexOfTypeA = i;
            }
            else if(lastIndexOfTypeB < 0)
            {
                lastIndexOfTypeB = i;
                typeB = tree[i];
            }
            else if(tree[i]==typeB)
            {
                lastIndexOfTypeB = i;
            }
            else // tree[i] is a 3rd type
            {
                maxLength = Math.max(maxLength, i-startOfWindow);
                if(lastIndexOfTypeA < lastIndexOfTypeB)
                {
                    startOfWindow = lastIndexOfTypeA+1;
                    typeA = tree[i];
                    lastIndexOfTypeA = i;
                }
                else
                {
                    startOfWindow = lastIndexOfTypeB+1;
                    typeB = tree[i];
                    lastIndexOfTypeB = i;
                }
            }
            
            ++i;
        }
        
        return Math.max( maxLength, i-startOfWindow );
    }
}


Runtime: 5 ms, faster than 99.82% of Java online submissions for Fruit Into Baskets.
Memory Usage: 48.4 MB, less than 84.46% of Java online submissions for Fruit Into Baskets.