Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!

Example:

Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6

Problem Clarification

The image clarifies it.

Idea – 1

We consider how much water we can trap considering a certain bar as the right end, how far left do we need to go to find the left end? Of course we need to subtract the area of the inbetween bars.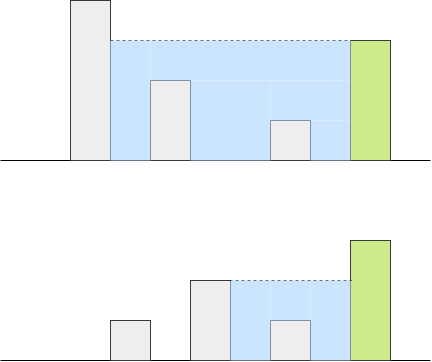

From the figure above, we see we need to go left until we find a bar that has same or higher height than the right end bar or in case all bars to the left are shorter in height we take the tallest among them. So, for each index j, if we precompute which index i to its left has the biggest height then in one pass from right to left we can compute the total trapped water. Time and space .

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        
        // need at least 3 indices to trap some water
        if(n < 3)
        {
            return 0;
        }
        
        int[] maxIndex = new int[n];
        maxIndex[0] = 0;
        for(int i = 1; i < n; ++i)
        {
            if( height[i] > height[maxIndex[i-1]] )
            {
                maxIndex[i] = i;
            }
            else
            {
                maxIndex[i] = maxIndex[i-1];
            }
        }
        
        int water = 0;
        
        // j is the index of right end bar
        // i would be the index of left end bar
        // min height of these two ends would define
        // height of the rectangle
        //
        int j = n-1;
        while(j > 1) // need at least three indices to trap some water
        {
            int i = j-1;
            int leftEnd = maxIndex[i];
            int inbetweenArea = 0;
            while(i > leftEnd)
            {
                if(height[i] >= height[j])
                {
                    break;
                }
                
                inbetweenArea += height[i];
                
                --i;
            }
            
            int w = j-i-1;
            int h = Math.min( height[i], height[j] );
            water += (w*h - inbetweenArea);
            
            // left end of previous rectangle
            // becomes right end of the new rectangle
            //
            j = i;
        }
        
        return water;
    }
}


Runtime: 1 ms, faster than 99.92% of Java online submissions for Trapping Rain Water.
Memory Usage: 38.9 MB, less than 81.28% of Java online submissions for Trapping Rain Water.

Idea - 2

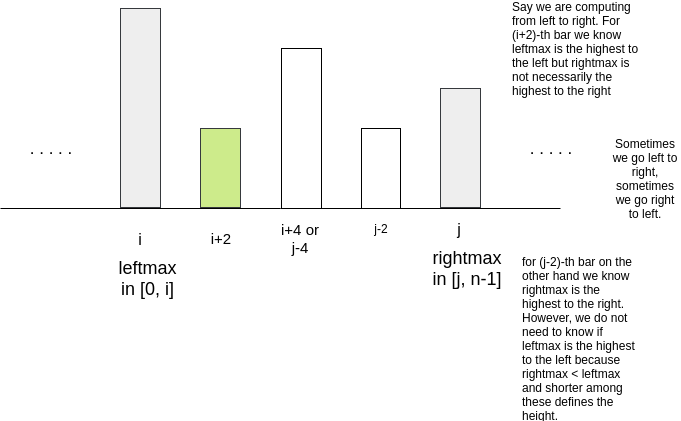
We consider how much water a bar can hold on top of it, summing these up would give the result. For a given bar we are only interested in the highest bar to its left and the highest bar to its right, because the shorter among these two would determine how high the water can stay on the given bar.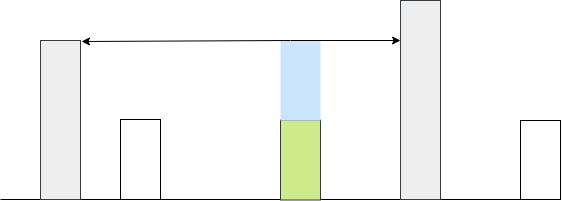

To update leftmax (highest bar to the left) and rightmax (highest bar to the right) we keep switching directions as needed. This gives us a time and space algorithm.

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        
        // need at least 3 indices to trap some water
        if(n < 3)
        {
            return 0;
        }
        
        int water = 0;
        int leftmax = 0, rightmax = 0;
        int i = 0, j = n-1;
        while(i < j)
        {
            if(height[i] < height[j]) // keep going left to right
            {
                leftmax = Math.max(leftmax, height[i]);
                water += (leftmax-height[i]);
                ++i;
            }
            else // switch direction, go right to left
            {
                rightmax = Math.max(rightmax, height[j]);
                water += (rightmax-height[j]);
                --j;
            }
        }
        
        return water;
    }
}


Runtime: 1 ms, faster than 99.92% of Java online submissions for Trapping Rain Water.
Memory Usage: 37.7 MB, less than 94.17% of Java online submissions for Trapping Rain Water.