Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

Input: "cbbd"
Output: "bb"

class Solution {
    public String longestPalindrome(String s) {
        
    }
}

Problem Clarification

The longest palindromic substring must have characters that are adjacent in the original string.

Idea - 1

We can check each of the substrings and see if it is palindromic in time and keep track of the longest among them. Total time is and space is .

class Solution {
    public String longestPalindrome(String s) {
        
        int n = s.length();
        if(n == 0)
        {
            return "";
        }
        
        int maxLength = 1;
        int longestStart = 0, longestEnd = 0;
        for(int i = 0; i < n-1; ++i)
        {
            for(int j = i+1; j < n; ++j)
            {
                if(palindromic(s, i, j) && j-i+1 > maxLength)
                {
                    maxLength = j-i+1;
                    longestStart = i;
                    longestEnd = j;
                }
            }
        }
        
        return s.substring(longestStart, longestEnd+1);
    }
    
    private boolean palindromic(String s, int begin, int end)
    {
        while(begin < end)
        {
            if(s.charAt(begin) != s.charAt(end))
            {
                return false;
            }
            
            ++begin;
            --end;
        }
        
        return true;
    }
}


Runtime: 1541 ms, faster than 5.00% of Java online submissions for Longest Palindromic Substring.
Memory Usage: 37.3 MB, less than 94.27% of Java online submissions for Longest Palindromic Substring.

Idea - 2

If is a palindrome, then it follows that and is a palindrome. So, if we find out which 2-length substrings are palindrome then finding if a 4-length substring is a palindrome take time. So, overall we need to find which of the substrings are palindrome and each can be checked in time making overall time complexity and space complexity as well.

class Solution {
    public String longestPalindrome(String s) {
        
        int n = s.length();
        if(n == 0)
        {
            return "";
        }
        
        boolean[][] dp = new boolean[n][n];
        
        // all 1-length substrings are palindromes
        for(int i = 0; i < n; ++i)
        {
            dp[i][i] = true;
        }
        
        int maxLength = 1;
        int longestBegin = 0, longestEnd = 0;
        for(int length = 2; length <= n; ++length)
        {
            int i = 0;
            while(i+length <= n)
            {
                int j = i+length-1;
                // i-th and j-th char match and these are the only chars or
                // the in between chars form palindrome
                if(s.charAt(i)==s.charAt(j) && ( i+1 > j-1 || dp[i+1][j-1] ))
                {
                    dp[i][j] = true;
                    
                    if(length > maxLength)
                    {
                        maxLength = length;
                        longestBegin = i;
                        longestEnd = j;
                    }
                }
                
                ++i;
            }
        }
        
        return s.substring(longestBegin, longestEnd+1);
    }
}


Runtime: 46 ms, faster than 40.03% of Java online submissions for Longest Palindromic Substring.
Memory Usage: 39.4 MB, less than 19.86% of Java online submissions for Longest Palindromic Substring.

Idea - 3

A palindrome can be checked starting at two ends and going inwards or starting at a center going outwards. The latter approach has the benefit that there are only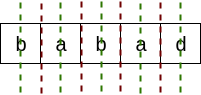 centers, so we end up with an algorithm with time and space . Centers are of two types: falls on a character, falls between two characters.

class Solution {
    
    class IndexPair
    {
        int i, j;
        public IndexPair(int i, int j)
        {
            this.i = i;
            this.j = j;
        }
        
        public int length()
        {
            return j-i+1;
        }
    }
    
    public String longestPalindrome(String s) {
        
        int n = s.length();
        if(n == 0)
        {
            return "";
        }
        
        int maxLength = 1;
        IndexPair sol = new IndexPair(0, 0);
        for(int center = 0; center < n; ++center)
        {
            IndexPair candidate = longestFromCenter(s, center);
            if(candidate.length() > sol.length())
            {
                sol = candidate;
            }
        }
        
        return s.substring(sol.i, sol.j+1);
    }
    
    private IndexPair longestFromCenter(String s, int center)
    {
        int n = s.length();
        
        // falls on a character
        int left1 = center-1;
        int right1 = center+1;
        while(left1 >= 0 && right1 < n && s.charAt(left1)==s.charAt(right1))
        {
            --left1;
            ++right1;
        }
        
        int length1 = right1-left1-1;
        
        // falls between two characters
        int left2 = center-1;
        int right2 = center;
        while(left2 >= 0 && right2 < n && s.charAt(left2)==s.charAt(right2))
        {
            --left2;
            ++right2;
        }
        
        int length2 = right2-left2-1;
        
        if(length1 > length2)
        {
            return new IndexPair(left1+1, right1-1);
        }
        else
        {
            return new IndexPair(left2+1, right2-1);
        }
    }
}

Runtime: 14 ms, faster than 64.48% of Java online submissions for Longest Palindromic Substring.
Memory Usage: 37.1 MB, less than 95.43% of Java online submissions for Longest Palindromic Substring.